Activity feedback

I gave at least a half mark for any submission, but next time, incomplete submissions will receive a zero.

  • You need to use the template from the isdas package.
  • You need to submit knitted PDFs.
  • You should finish all the coding parts in the lab activities submission.
  • You need to answer all the questions in the activity sections (highlights and threshold concepts are optional) in the in-class activity submission.
  • Some submissions have errors in the YAML header, causing the PDF to not use the correct template.
  • We have two activities each week, and you need to submit both in each submission.
  • You need to submit both PDFs in the same submission.

Line breaks in markdown

Simply changing a line in Markdown won’t create a line break.

Unlike \(\LaTeX\) (\newline) or HTML (<br>), Markdown does not have explicit line break syntax.

The following example would produce a single line sentence after knitting:

first line of text
still the first line of text


In Markdown, line breaks are created implicitly using empty lines.

The following example would produce two lines after knitting:

first line of text

second line of text

Packages we use today

Load the following three packages.

library(isdas)
library(sf)
library(tidyverse)
library(spatstat)

If you have trouble restoring the reproducible environment, you need to manually install the packages first.

install.packages("remotes")
remotes::install_github("paezha/isdas")

install.packages("sf")

install.packages("tidyverse")

install.packages("spatstat")

New package for today: spatstat

spatstat is an R package for spatial statistics with a strong focus on analyzing spatial point patterns in 2D.

You can find documentation for this package at:

Random vs. deterministirc process

Let’s denote the probability of an event occurring at point \((x,y)\) as \(Prob(Event_{(x,y)})\). The points are located within a unit square ranging from 0 to 1.

  • A random process: \(Prob(Event_{(x,y)}) = B(n = 1, p = 0.5)\)
  • A deterministic process:
    \(Prob(Event_{(x,y)}) = x\)
  • A stochastic process: \(Prob(Event_{(x,y)}) = x - x \cdot B(n = 1, p = 0.5)\)

Generate random values from a distribution

There is a family of functions that start with r* capable of generating random values from a given distribution.

From a nomral distribution:

rnorm(n = 5, mean = 0, sd = 1)
[1]  0.5185718 -0.5801848  1.7541242 -1.4321465 -1.3573983

From a binomial distribution:

rbinom(n = 5, size = 1, prob = 0.5)
[1] 0 1 0 1 0

These functions are very useful for simulations.

Random number generator and seed

In computers, there is no true random number generator; they all use pseudo-random number generators. This means that the random numbers produced by computers are just the output of a very complex function based on an input, or seed.

As a result, if we know the seed, we can perfectly predict the random numbers generated by a computer’s random number generator.

Typically, computers use the current time as the seed (R uses this approach).

Setting a seed in R

You can control the random number generation algorithm by setting a seed value in R.

set.seed(437988)
rbinom(n = 5, size = 1, prob = 0.5)
[1] 1 0 0 0 1
set.seed(437988)
rbinom(n = 5, size = 1, prob = 0.5)
[1] 1 0 0 0 1

Note that the seed in R is actually a vector, a sequence of values, and set.seed changes this vector to a particular state.

If you do not set the seed again before rerunning the second rbinom, it will produce different results.

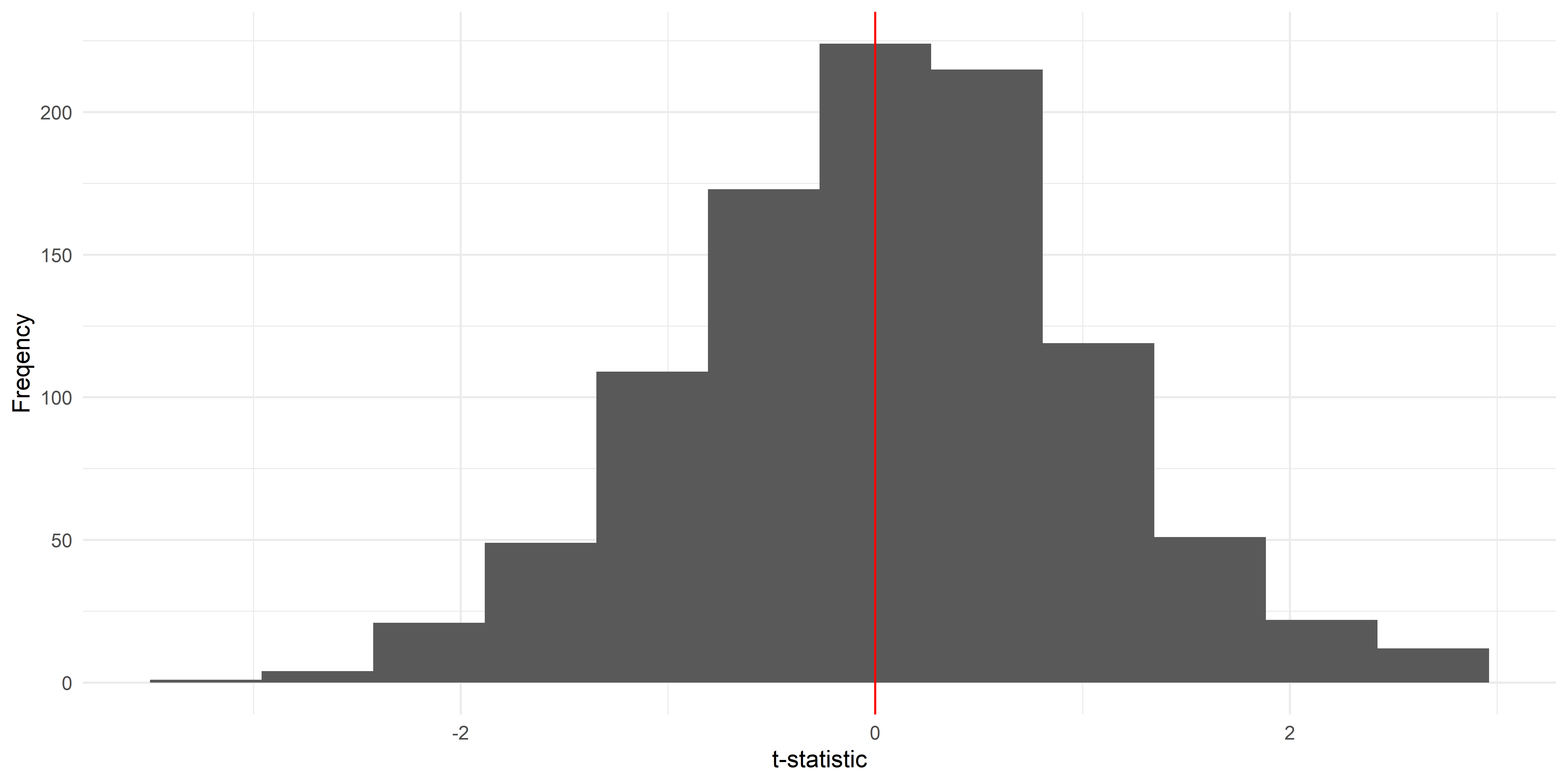
What is \(p\)-value?

Let’s say we have two samples from two different distributions. We want to perform a statistical test to compare their means (\(H_1: \overline{x_1} \neq \overline{x_2}\)). The \(p\)-value is the area under the curve that is more extreme than the test statistic, multiplied by 2.

Activities for today

  • We will work on the following chapter from the textbook:
    • Chapter 8: Activity 3: Maps as Processes
    • Chapter 10: Activity 4: Point Pattern Analysis I
  • The hard deadline is Friday, January 31 (12:00 pm).