Histogram binwidth
- Binwidth has nothing to do with bandwidth in Kernel density.
- Binwidth simply controls for the size of breaks in the histogram.
\(\hat F\)-function
Empty space distances:
\[d(u, \mathbf x) = \min\{\Vert u - x_i \Vert : x_i \in \mathbf x\}\] from a fixed location \(u \in \mathbb R^2\) to the nearest point in a point pattern \(\mathbf x\) is called the empty space distance or void distance.
The empty space function \(F\):
\[ \hat F(r)= \frac{1}{m}\sum_{j}\mathbf{1}\{d(u_j, \mathbf x) \le r\} \]
The \(F\)-function measures the distribution of all distances from an arbitrary reference location \(u\) (random or evenly distributed) in the plane to the nearest observed event \(u\).
\(\hat K\)-function
\[ \hat K(r) = \frac{1}{\hat\lambda \text{ area}(W)}\sum_i\sum_{i \ne j}\mathbf 1\{\Vert x_i-x_j \Vert \le r\} \]
where \(\hat\lambda\) is the estimated intensity of the point patterns.
Of the distance-based techniques that you have seen so far, \(\hat G\) and \(\hat F\) are often used as complements. The \(\hat K\) is useful when exploring multi-scale patterns.
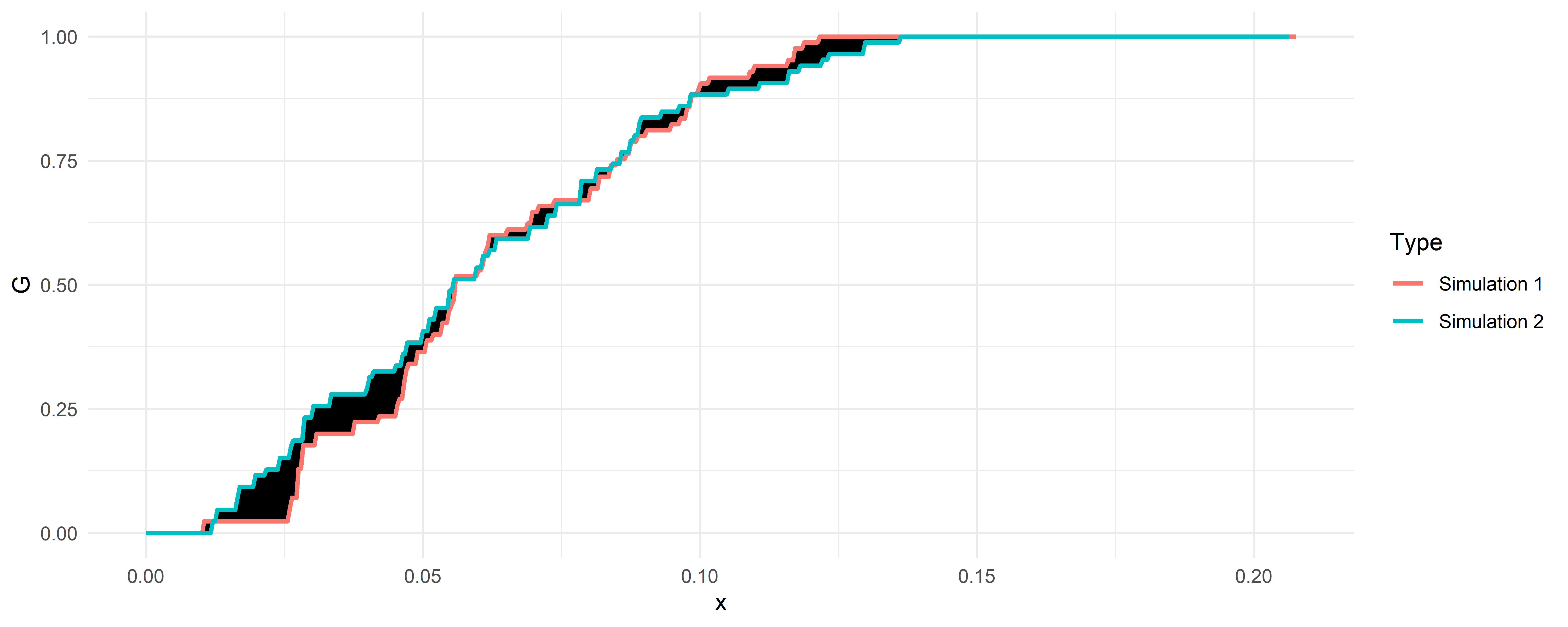
Simulation to obtain a confidence interval
Given the challenge of solving for the standard deviations of test statistics, we employ simulations to derive a confidence interval.
Activities for today
Reference
2025 Zehui Yin